
#Diffraction limit calculator plus#
Generally speaking, samples vary in thickness and they vary in flatness, so focusing is required.įor 20X magnification, which can be a numerical aperture of 0.6 to 0.8, the depth of field drops to about plus or minus 500 nanometers. In that case, if the sample is very flat, focusing may not be required at all, or only one needs to happen one time. For a low magnification objective such as a 4X or even a 10X, the typical depth of field is plus or minus 3 to 5 microns. For water, it’s refractive index is 1.33, and specialized immersion oil for microscopy is 1.52. In most cases the material between the objective and sample is air, and “n” equals 1.00. “n” is the refractive index of the material between the objective and the sample Generally speaking, for any given objective, it is worth it to pay to get the highest possible numerical aperture, but there is a slight downside to that. By using bluer light, the resolution can be increased, but for a particular application, that may not be possible. There is one other variable that can be adjusted. That is why numerical aperture is the key to high-resolution imaging. If the objective doesn’t collect a wide-angle of the cone, for example, a long working distance, low power objective will merely be getting the light that’s going straight through. The way to do that is to have a high numerical aperture, a big wide cone. The sample is throwing light out in all directions and the job of the objective is to collect as much of that light as possible. This describes what the fine structure of your sample is doing, it could be cells, chromosomes, or nuclei, and all of that fine structure spreads the light out. Unless the objective is capturing all of those higher orders, it is difficult to synthesize a high-resolution image.
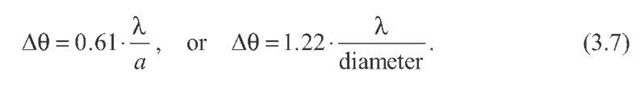
As shown in the diffraction image, the brightest light is the zero-order straight through, then the intensity decreases for the first order, second order, third order, etc. What actually happens is due to the wave nature of light, the light is diffracted, and instead of going straight, it spreads out into a cone. If a pinhole is illuminated with some light, the light would be directed in a straight beam. To better understand diffraction imagine if light moved strictly in straight lines. While some oversampling is appropriate, 4 times is excessive and a waste of sensor pixels. Therefore, the resolution of the sample is > 4 times the geometric resolution at the camera sensor which results in oversampling. Using the above equation, the diffraction limited resolution is actually 419 nm. For example, yellow green light has a wavelength lambda of 550 nm. However, due to diffraction, the sample image resolution will be greater than 100 nm. The sensor and magnification provide 100 nm geometric resolution. In the previous example we considered a sensor with 4 micron pixels used with an objective with 40X magnification and a numerical aperture of 0.8.

The formula for diffraction limited resolution is: To better understand how that works, we need to explore another concept which is called numerical aperture. The wave nature of light leads to a condition called diffraction and due to diffraction, limits are set on resolution. There’s a property of light which is that in addition to acting like a particle, the photon, it also has a wave property. But it turns out it isn’t quite that simple.

For example, a sensor with 4 micron pixels and a 40X objective, would be 0.1 micron of geometric resolution or 100 nanometers.
In addition to the magnification reducing the size of the sensor down to the size of the field of view on the sample, it also does the same with the pixels. This size FOV is typical for microscopy applications. If the sensor diagonal is 20 mm and if the magnification of the objective is 20X then divide the sensor size by magnification to get a Field Of View (FOV) of 1 millimeter.
#Diffraction limit calculator tv#
In all of these cases, the sensor has a particular size and is typically referred to by its diagonal measure (similar to specifying a TV size).


 0 kommentar(er)
0 kommentar(er)
